 |
|
|
|
[原创] 信息加密技术实用算法的研究与开发——无密钥加密模式初探
[ 2007-11-03 13:37:32 ]
引言/提要：本文介绍了信息加密技术之中，一种不常见但很有前途的模式——无密钥加密模式。通过与其他通用加密模式的比较，探讨了该模式的运作原理，及其在不安全信道中保护信息的技术可行性和实用性。同时，从比较中初步反映出该模式与其他加密模式之间的优缺点。
关键词：现代密码学，无密钥加密模式，加密技术，信息安全
摘要
本文介绍了信息加密技术之中，一种不常见但很有前途的模式——无密钥加密模式。通过与其他通用加密模式的比较，探讨了该模式的运作原理，及其在不安全信道中保护信息的技术可行性和实用性。同时，从比较中初步反映出该模式与其他加密模式之间的优缺点，进而论述不同的加密模式如何优势互补。
本文内容的划分：1、信息加密技术的价值；2、加密模式的区分；3、几种加密模式的概念模型；4、加密算法的数学理论基础；5、无密钥模式的可行性研究；6、无密钥模式的增强；7、与其他加密模式的比较；8、不同加密模式的转化与结合。
目录：
1、信息加密技术的价值
2、加密模式的区分
3、几种加密模式的概念模型
4、加密算法的数学理论基础
5、无密钥模式的可行性研究
6、无密钥模式的增强
7、与其他加密模式的比较
8、不同加密模式的转化与结合
信息加密技术的价值
本文所讨论的信息加密技术，是指利用计算机、密码机等智能信息工具，通过一定的算法，对数字化的信息进行加密变换，从而保障信息安全的技术。
信息加密技术，具有十分广泛的用途。典型的应用包括：互联网应用，如电子邮箱、即时通信、网页浏览等；电信业务，如IP电话、电视会议、短信等；商业用途，如公文传发、银行支付、网间结算等。这些应用涉及大量有价值的信息，需要得到真正强有力的加密技术的保护。
反过来，加密技术也促进了信息应用的发展，能够使应用领域扩展到前所未有的范围。例如，IP电话本来存在易被窃听的弱点，应用范围有限。一旦采用了加密技术，窃听的难度等同于破解密码，而且可以加入数字身份认证等特性。如此一来，IP电话就可以应用到商业领域，大大提高了IP电话的价值。
加密技术对于个人隐私、商业利益乃至国家安全，都有着相当重要的意义。只要看看国外对加密技术的重视程度，就会明白这一点。与直接进口国外现成加密产品相比，自主开发的核心技术有着特殊的价值。使用进口产品固然可以节省研发时间，但完全依赖进口也是不安全的。
首先，自主核心技术可以打破进口技术垄断。美国长期对强加密技术实行出口管制，外商也会出于自身利益而保护核心技术，从而阻止我们在技术上的超越。只有自主开发核心加密技术，才能够缩短差距，打破垄断，防止受制于人，并以竞争拉低进口产品的价格。
其次，自主核心技术在安全性上更可信。由于进口产品的核心技术掌握在外商手中，难保里面不留有后门，或者连他们自己都不发觉的缺陷。例如，至今仍不清楚DES算法中，美国政府修改过的S转换盒是否内含玄机。而自主开发的核心技术有没有后门，是否存在隐患，自己一清二楚。
算法公开的加密技术，是现代密码学的主要研究对象。因为算法不公开的加密，依赖于算法的不透明来维持保密性，无法从理论上保障其安全。一旦算法暴露，安全性也就不复存在了。而算法公开的加密技术，则是在算法本身不是秘密的情况下，仍然能够保持加密的安全性。这是真正经得起考验的加密技术，因此也是商业领域加密应用的主流。本文所讨论的加密技术，以算法公开的技术为主。
加密模式的区分
现代密码学中，把算法公开的加密技术分为单密钥模式、双密钥模式和无密钥模式几种。其中前两者是最常见的模式，而无密钥模式由于设计难度大，虽然是一种理想的加密通信模式，却未能得到广泛的应用。
单密钥模式，也称为私钥模式、对称密钥模式，是通信双方使用同一个密钥的加密模式。常见的3DES、AES标准，就属于单密钥模式。
双密钥模式，也称为公钥模式、非对称密钥模式，是通信双方使用两个不同密钥的加密模式。其中一方使用的密钥是公钥，公钥可以对外公开，另一方使用的密钥是自己的私钥，私钥是保密的。常见的RSA算法、椭圆离散对数算法，就属于双密钥模式。
无密钥模式，也称为随机密钥模式，通信双方并不使用固定的密钥，而是每次都各自随机生成一个密钥，用过一次就不再使用。无密钥模式并不是没有密钥，更不等于不保密，相反由于每次都采用随机密钥，而且只使用一次，这恰恰是最安全的。因为每次加密被破解，都不会影响到其他各次的加密，只因密码不同。
目前比较常用的是公钥模式，其中的典型就是RSA算法，这是基于大质数分解数学难题的加密算法。许多流行的安全通信、数字签名、认证中心等应用，都采用了RSA加密。由于RSA算法的速度问题，通常都与速度较快的单密钥算法结合使用：用RSA算法进行数字签名和传送单密钥算法的密码，而实际的大量信息内容则用单密钥算法进行加密。
事实上，加密模式不是孤立存在的，必然依赖于加密算法。一种加密模式可以有多种不同的加密算法。另一方面，加密算法并不局限于特定的加密模式。同一种加密算法，有可能既适用于某种模式，又适用于另一种模式。
几种加密模式的概念模型
为了说明这几种加密模式的区别，我们可以对这几种加密模式作个比喻。
假设甲乙两人进行秘密通信，任务是甲要把某些机密信息传递给乙。但是双方之间的信息传输通道是不安全的，例如是通过互联网或电话线来通信，别人随时可以截取到通信的信息。为此，甲乙两人对信息进行了加密，使得别人即使截取到信息，也因为难以破解而无法得知里面的内容。
我们分别描述甲乙两人用单密钥模式、双密钥模式、无密钥模式来进行秘密通信的情形。
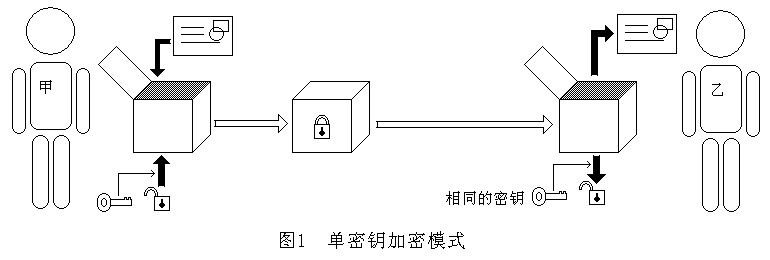
单密钥模式就好像是一个带锁的匣子，甲乙双方各有一把相同的钥匙，都可以打开这把锁。
通信过程是：甲把信放进匣子，用钥匙锁上锁，然后把匣子邮寄给乙。运输途中匣子是锁着的，因此信是安全的。乙收到匣子后，用钥匙开锁，打开匣子，就取到了信。
单密钥模式的概念模型如图一所示。
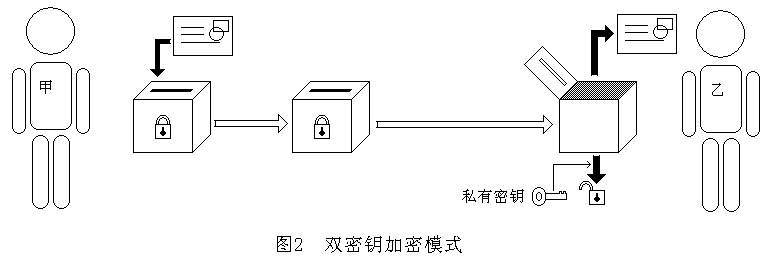
双密钥模式就好像是一个信箱，上面有一条细缝，可以把信投进信箱里，但是无法从细缝里取出里面的信。信箱后面还有一个加锁的门，打开门就可以取到信。锁的钥匙只有乙才拥有。
通信过程是：甲把信从细缝塞进信箱里，然后把信箱邮寄给乙。运输途中信箱是锁着的，从细缝里也取不出来，因此信是安全的。乙收到信箱后，用钥匙开锁，打开信箱门，就取到了信。
双密钥模式的概念模型如图二所示。
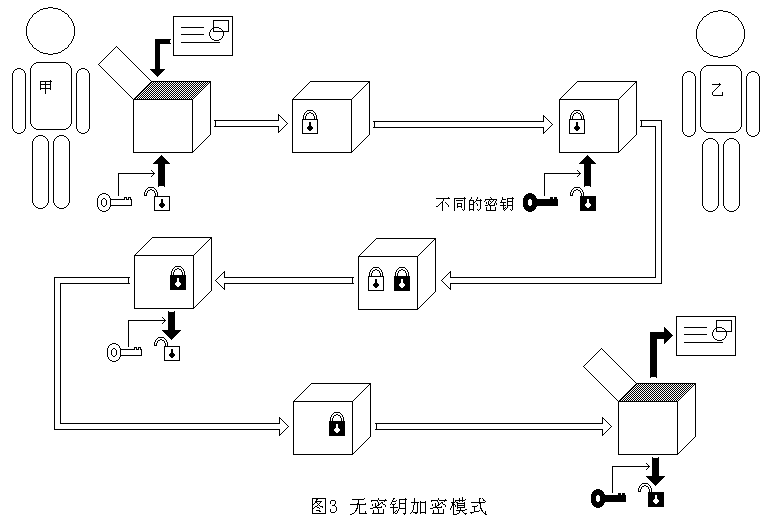
无密钥模式就好像是一个带两个锁眼的匣子，任何锁都可以扣在锁眼上。而只要任何一个锁眼扣上锁，匣子就打不开。
通信过程会复杂一些：
首先甲把信放进匣子，随意找一把锁和钥匙，用锁扣住锁眼A，把匣子邮寄给乙。运输途中因为锁眼A上了锁，匣子打不开，因此信是安全的。
乙收到匣子，也随意找一把锁和钥匙，用锁扣住锁眼B，把匣子寄回给乙。运输途中因为锁眼A、B都上了锁，匣子打不开，因此信是安全的。
甲收到匣子，用钥匙打开锁眼A上的锁，再把匣子寄回给乙。运输途中因为锁眼B仍然上了锁，匣子打不开，因此信是安全的。
乙收到匣子，用钥匙打开锁眼B上的锁，打开匣子，就取到了信。
无密钥模式的概念模型如图三所示。
以上概念模型，描述信在运输途中是“安全”的，其实都忽略了这样一个事实：别人可以用暴力砸开信箱、匣子，取到里面的信。但是，我们仍然说信是“安全”的，这是一种相对的安全。因为信箱、匣子如果足够坚固，暴力砸开它需要付出极大的代价，即使取到信也是得不偿失。
现代密码学认为：没有绝对的安全，安全只是相对而言。只要破解保护所付出的代价，超过或者相当于受保护信息的价值，我们就说受保护的信息是安全的。
加密算法的数学理论基础
信息加密作为实用的技术，可以采用的理论基础并不唯一。本文所涉及的加密算法与数学难题有关，而选用的理论基础也是数学上的函数理论。
我们把加密、解密的运算看作是某种可逆的函数，其中解密是加密的逆函数。而且，这种函数有着如下特征：加密函数的运算很容易，并且密钥是函数中的一个参数。解密作为加密的逆函数，密钥同样是参数之一。而最为重要的一点，在知道密钥的情况下，解密函数的运算很容易，如果不知道密钥，解密运算将非常困难。
加密容易、解密容易、破解困难，正是这样的特征，才使得加密信息得到保护，不会轻易被外人获取，从而使得加密算法具有了信息安全的价值。
以上论述，若以整数域里的二元函数为例，可以用数学方式来描述如下：
设x是未加密的明文，y是加密后的密文，a是加密密钥，b是解密密钥，x、y、a、b都是整数。设加密函数f(x, a)、解密函数g(y, b)都是整数域里的函数，g是f的逆函数。
加密过程：y=f(x, a)。
解密过程：x=g(y, b)=g(f(x, a), b)。
破解过程：有多种途径，可以是求解下述方程之一。至于方程中哪个是未知数，哪个已知，则视情况而定。
(1)求解方程y=f(x, a)，(2)求解方程x=g(y, b)，(3)求解方程x=g(f(x, a), b)。
函数f、g的运算应该是容易的，而求解上面任何一个方程都应该是困难的。理想情况下，只能用穷举法求得方程的解，这样的加密算法最为成功。
以RSA算法为例，f、g都是乘法和求模运算的函数，比较容易计算，而解方程则需要用到质数分解运算。在质数很大的情况下，这种运算是非常困难的，因此RSA算法是个好的加密算法。
应当注意，加密和解密的密钥a、b可以相等，也可以不等。当a=b时，就是单密钥加密模式，否则就是双密钥或多密钥模式。
以上就是加密算法的数学理论基础。理论上，任何具备上述特征的数学函数，都可以用来作为加密算法。而实际上，由于受到现实硬件性能、软件算法、经济成本等条件的限制，许多数学算法实现起来并不理想，所以不实用。
无密钥模式的可行性研究
从概念模型来看，无密钥模式其实是相当理想的，甚至比双密钥模式还要好。因为双密钥模式尚且需要管理公钥和私钥，而无密钥模式根本没这个必要，每次只要随机产生一个密钥即可。这种模式之所以没有广泛流行，很大程度上是因为难以设计出适用于该模式的加密算法。
如前所述，这样的加密算法必须具备加密容易、解密容易、破解困难的基本特点，不能有缺陷。而无密钥模式下，至少需要进行4次加解密运算、3次信息交换，很容易存在破解的漏洞。某些算法能够满足无漏洞、难破解的要求，却又因运算复杂，导致现实情况下加密或解密的速度太慢，无法满足实用性要求。某些算法的加、解密速度足够快，但破解的速度又不够慢，导致加密强度不足，同样满足不了实用性要求。
可见，研究出适当的加密算法，并且开发出现实可行的计算机程序，是实现无密钥模式的基本前提。该模式的可行性，取决于其加密算法的可行性。
笔者经过长时间的思考，并参考了有关加密算法的资料，发现基于离散对数难题的加密算法，可以很好地满足无密钥模式的要求。随后，开发出关键算法程序，并进行了精心优化。经过测试和分析，加密效果令人满意。
在测试环境下，采用AthlonXP 1800+的普通32位PC机，3217位加密的时间不超过1.5秒，而1279位加密更达15倍的速度，低于100毫秒。解密速度与加密相同。如果采用64位算法，纯软件性能即可达到32位算法的2至4倍。考虑到当前已有更高性能的计算机硬件产品，甚至计算机集群、网格，还可以用DSP开发专用密码卡，这种加解密速度完全符合实用性要求。
离散对数加密，是基于数学难题——求解以质数为模的自然数对数而设计的加密算法，其加密强度与RSA算法相当，没有明显的缺陷，能够满足信息保密的要求。
至此，有了理论基础及具体算法，又有了实际程序及测试数据，无密钥加密模式的现实可行性已初步确定。
无密钥模式的增强
为进一步提高加解密速度，借鉴了RSA结合3DES的方式，把离散对数加密算法与单密钥算法相结合。前者负责传递后者的密钥，后者则负责加密明文信息。
理论上，任何单密钥算法，包括标准的3DES在内，都可以与前者配合使用。实际中，选用了同样是自主开发的一种单密钥算法。该算法采用384位长分组的链式加密，明文经过充分糅合，达到位扩散的效果，能够较好地对抗线性分析、差分分析攻击。
根据信息性质的不同，明文在加密之前，还可以选择性地进行有损或无损压缩，增加信息熵的无序性，可有效对抗概率统计分析攻击。
经过以上处理，已经足以抵御攻击者窃取信息的努力，保障信息的保密性。但是，对于攻击者的身份冒充、信息破坏等手段，仍尚未能够有效防御。
这就是说，加密信息通过不安全的途径进行传递，攻击者也已经无法在合理时间内破解。但是，如果攻击者冒充通信双方的身份，实施中间人攻击，真正的通信方会被欺骗。又或者，攻击者虽然破解不了，但可以篡改、删除、重发密文，而接收方不会发觉。
这些攻击并不是无法抵御的，我们可以从流行的加密认证体系中得到借鉴，运用到自己的无密钥模式之中。
给明文加上序列号、时间戳，则一旦信息被删除、重发，或者颠倒了发送顺序，就可以从序列号和时间戳上发觉。给明文加上摘要，也就是明文的校验码，则一旦信息被篡改，会导致摘要不符，从而暴露。当然，序列号、时间戳和摘要必须连同明文一起加密。
理论上，任何一种摘要算法都可以应用在无密钥模式之下。实际中，选用了自主开发的散列算法，是基于离散幂运算的。之所以选用这样的算法，是考虑到加密算法同样用到了离散幂运算，这样在设计硬件加密芯片的时候，可以重复利用相同的逻辑部件，简化设计，降低硬件成本。
要防止身份冒充，可以采用数字签名算法。数字签名应满足以下要求：可鉴别，对方可以从数字签名中判断出真假。防冒充，别人不知道密钥，在合理时间内将无法伪造出符合条件的数字签名。防抵赖，作过的数字签名不会出自别人。防泄漏，从数字签名中不会有足够的信息，令密钥外泄。
目前在无密钥模式下，仍然采用双密钥模式的数字签名。原因是无密钥模式中的密码全是随机生成，并不固定，而数字签名却要求具有固定的特征，才能够认证签名者的身份。双密钥模式，有用作签名的私钥和用作验证的公钥，确实适合数字签名。
理论上，任何一种数字签名算法，包括RSA算法，均可应用在本文所描述的密码体系之下。实际中，选用了一种自主开发的算法。该算法原本由国外设计，用于当前的双密钥加密模式，只有算法简介，没有现成的程序。笔者对其算法稍作修改，使之适于作数字签名之用，然后自主开发全部的程序代码。该数字签名算法同样基于离散对数难题，如前所述，选用该算法可以简化硬件加密芯片的设计，节约成本。
经过上述切实有效的增强工作，无密钥加密模式已经形成较为严密的防御体系，可以抵抗大部分针对信息的攻击，能够满足多种实际应用的需要。不过，安全永远是相对的，目前流行的加密模式不能例外，这里的无密钥模式同样不会例外。我们只可以说，够用就好。只要我们所提供的安全保护，能迫使攻击者不得不付出足够的代价，我们就成功了。
与其他加密模式的比较
当无密钥模式被设计成相对完善的密码体系之后，我们再回过头来看看，这种模式与其他模式相比，有什么优点和不足。
单密钥模式的优点在于加解密速度快，破解困难。单密钥模式的加密算法比较容易设计，只要是精心设计过的好算法，在密钥长度相同的条件下，单密钥模式的加解密速度、加密强度都是三种模式之中最高的。
而单密钥模式的不足也很明显，就是密钥在传送、管理上的困难。另外，由于双方共用相同的密钥，很难实现数字签名、身份认证等功能。
双密钥模式的优点，就在于密钥的管理和传送方便。由于有公钥和私钥，并且前者无法计算出后者，因此可以将公钥向所有人公布，而只保管一个私钥。不象单密钥模式，和多少人通信就需要保管多少个不同的密钥。另外，双密钥模式十分适用于数字签名和身份认证。
至于双密钥模式的不足，在于加解密速度和生成密钥的速度较慢。尤其是后者，要生成一对密钥是比较费力的。以RSA算法为例，生成密钥需要寻找大质数，需要计算乘法逆元，这些都是相当耗时、耗计算机资源的运算。
无密钥模式的最大优点就是无密钥——确切地说是没有固定的密钥。不象双密钥模式，无密钥模式是不需要保存密钥的，每次加密都随机生成新的密钥。因此，泄漏密钥的危险性大大减小，也节省了密钥管理和传送的成本。可以说，无密钥模式是三种模式之中最易用的。
但是，无密钥模式也存在不足。首先是算法设计困难，既要让双方能够用真正随机的密钥完成通信，又要防止出现漏洞，泄露密钥，还要满足现实的要求，光是设计这样的算法就需要毅力、能力和运气。其次，该模式要进行3次通信，须消耗一部分带宽资源。还有，目前所用的离散幂运算的速度较慢，使加解密速度比RSA算法还要慢。不过，采用了精心优化过的算法之后，速度弱点已经得到有效的弥补。
此外，在数字签名和身份认证方面，双密钥模式仍然具有优势，因此无密钥模式的数字签名也借鉴了前者，采用随机生成的私钥和公钥作签名及认证。
不同加密模式的转化与结合
无密钥模式与双密钥模式，都是采用非对称的密钥。两者最大的区别，就在于密钥是否随机生成。换言之，如果每次加密都采用同样的非对称密钥，那就是双密钥模式，否则，每次都用不同密钥的就是无密钥模式。
因此，双密钥和无密钥模式之间，可以有条件地互相转化。无密钥模式下，若一旦生成密钥就固定不动，每次都用这对密钥加密，那就成了双密钥模式。反过来，双密钥模式下，如果每次加密都随机生成一对新密钥，将新的公钥传给对方用于加密，那就成了无密钥模式。
一般而言，无密钥模式转化为双密钥模式较容易，而反过来转化则较难。原因是双密钥模式的算法之中，生成一对密钥都比较费力，因此每次生成新的密钥就更不容易。而无密钥模式的算法易于生成密钥，采用固定的密钥也没什么困难。
例如RSA算法，每次寻找新的大质数和计算乘法逆元，代价相当可观，并不容易做到，因此RSA还是适合于双密钥模式，即一次性生成密钥，以后每次都采用这一对密钥。
至于前面所述基于离散对数难题的加密算法，则可适用于无密钥模式。因为该算法无须每次寻找大质数，仅需要每次生成随机数，实现的代价很小。纵使其数字签名采用了双密钥模式，该算法生成公钥和私钥的代价同样很小。
由于三种加密模式各有长处和不足，最好能够互相结合起来，取长补短。事实上，这完全可以实现。正如双密钥模式能够结合单密钥模式以加快速度，无密钥模式也可以。
前面所述无密钥模式的增强，实质上就是将三种模式很好地配合起来：无密钥模式负责传递密钥，单密钥模式负责加密信息，双密钥模式负责数字签名。
如此，三种模式的优势得以充分发挥：无密钥模式的密钥传递，保障了不安全信道之下，密钥的随机性和保密性；单密钥模式的信息加密，发挥了加解密速度和加密强度的优势；双密钥模式的数字签名，吸收了公钥体系在签名、认证方面的成熟之处。
由于无密钥模式在其中起了最关键的作用，因此三种模式结合之后，仍然归入无密钥加密模式的范畴。
以上对无密钥加密模式作了总体性的论述，具体每个环节的算法，须另文详尽介绍才能叙述清楚。目前，这仍是一种不常见的加密模式。但从简单比较中，我们已经可以知道该模式相对其他通用模式的优势所在。尤其是在随机密钥方面，该模式的安全性是其他模式所不可比拟的。
通过具体的加密算法，该模式被证实具有现实可行性，并且能够将几种加密模式的优势结合起来。考虑到性能、成本等多方面综合因素，无密钥加密模式很有发展前途。
信息安全领域里，没有绝对的安全，安全永远都是相对的。加密算法、加密模式并不会一成不变，总有改善和更新的时候。例如DES会被AES取代，以RSA为代表的双密钥模式又比纯单密钥模式应用得更为广泛。可以相信，以无密钥模式的优点，在信息安全领域里将会获得长足的进步，得到广泛的应用。
龙之梦
2004.11.11
|
|
|
相关文章：
 [原创] ISP技术在计算机组成原理实验仪中的应用（论文摘要） [2007-04-24]
[合著] 《计算机组成原理题解、题库与实验》实验教材原稿 [2007-04-24]
[合著] 实验参考 [2007-04-24]
[合著] 一台模型计算机的设计与调试（四）：组合逻辑控制器流水方案 [2007-06-27]
[合著] 一台模型计算机的设计与调试（三）：组合逻辑控制器方案 [2007-06-27]
[合著] 一台模型计算机的设计与调试（二）：微程序控制器流水方案 [2007-06-27]
最新留言：
 [2014-10-16]
[2014-10-16]
[2014-06-04]
[2014-06-04]
[2013-12-08]
[2013-11-29]
|
|
|
相关链接 |
|
|
人次